source("testing_dispersion_and_dependence.r")
# load packages
library(tidyverse)
library(haven)
library(ggplot2)
# Reading in the data
census_data <- read_dta("../datasets/01_census2016.dta")02 - ECON 325: Dispersion and Dependence
Outline
Prerequisites
- Introduction to Jupyter
- Introduction to R
- Introduction to Visualization
- Central Tendency
- Distribution
Outcomes
This notebook explains the concepts of dispersion and dependence. After completing this notebook, you will be able to:
- Understand and interpret measures of dispersion, including variance and standard deviation
- Understand and interpret measures of dependence, including covariance and correlation
- Investigate, compute, and interpret common descriptive statistics
- Create summary tables for variables, including qualitative variables
- Parse summary statistics for meaning
References
Introduction
In this notebook, we will continue learning about how to use descriptive statistics to represent sets of data. We’ve already seen how to compute measures of central tendency and determine which measures are appropriate for given situations. We’ll now focus on computing measures of dispersion and dependence in order to better understand both the variation of variables, as well as relationships between variables in a data set. We’ll dedicate time to both measures, but we’ll look at dispersion first. Let’s first import our familiar 2016 Census data set from Statistics Canada.
Understanding Measures of Dispersion
Measures of dispersion describe the spread of data, that is, the possible values that a variable in a data set can take on. Common measures of dispersion which we’ll look at include the range, interquartile range, standard deviation and variance.
Range and Interquartile Range
We’ve already seen the range and interquartile range in the Central Tendency notebook. Remember, the range is the difference between the maximum and minimum value that a variable takes on, while the interquartile range is the difference between the 75th and 25th percentile values. We can use functions like quantile() and fivenum() to calculate these statistics quite quickly.
Both functions return the same output: a list that includes the minimum value, 25th percentile, 50th percentile (median), 75th percentile, and maximum value. In this way, these commands allow us to construct a snapshot of both the spread of the middle 50% of data around the median (the interquartile range), as well as the spread of the data in its entirely (the range).
Variance
The variance is the average of the squared differences from the mean. A small variance indicates that observations tend to fall close to the mean, while a high variance indicates that observations are very spread out from the mean. The standard deviation (discussed next) is also the square root of variance, although we we won’t spend much time on variance here.
For example, a normal distribution with
mean = 30andsd = 5is exactly the same thing as a normal distribution withmean = 30andvariance = 25.
The biggest difference between the two is that the variance is a squared measure and does not have the same units as the data in the way that the standard deviation does; hence why we usually work with standard deviation instead.
Standard Deviation
The most commonly referenced measure of dispersion is standard deviation. This statistic measures dispersion around the mean. More specifically, it takes the squared value of the sum of the squared difference between each value and the mean for a given variable.
For drawn samples from the population:
\[ s_{x}^2 = \frac{\sum_{i=0}^{n} (x_i - \overline{x})^2}{n - 1} \]
\[ s_{x} = \sqrt{s_{x}^2} = \sqrt{\frac{\sum_{i=0}^{n} (x_i - \overline{x})^2}{n - 1}} \]
For the population:
\[ \sigma_{x}^2 = \int(x - \mu)^2 f(x) dx \]
\[ \sigma_{x} = \sqrt{\sigma_{x}^2} \]
Note: In general, we use samples to estimate population parameters and some samples have more information to estimate than others. For instance, an estimate of the population variance based on a sample size of 100 certainly has more information than a sample size of 10. The degrees of freedom is the amount of information an estimate has. The degrees of freedom for an estimate is equal to the number of observations minus the number of parameters we would like to estimate. Thus, the degrees of freedom of our estimate of variance (sample variance) is equal to n - 1.
In R, we can use the var() function to calculate the variance of a variable, and the sd() function for the standard deviation.
# calculate the variance of wage
variance <- var(census_data$wages, na.rm = TRUE)We can see the relationship between the standard deviation and the variance by taking the sqrt() of the variance to find the standard deviation below:
# fill in the ... with your code below to find the sd of wages
answer_6 <- ...(var(census_data$wages, na.rm = TRUE))
test_6()# recall the mean of wages
mean(census_data$wages, na.rm = TRUE) # remember that we need to remove all NA values otherwise R won't let us compute our summary statistics!
# calculate the standard deviation of wages
sd(census_data$wages, na.rm = TRUE) From the above, we can see that the standard deviation nicely comes in the same units as our variable of interest. It is also necessarily a positive or zero value. This convenience is partly why the standard deviation is such a preferred measure of dispersion.
Interpreting Variation
Let’s say we’re interested in understanding how the wages variable was dispersed around the mean.
In the case of wages above, we have a pretty high standard deviation, even higher than our mean! This tells us that most of the Canadians in the data set have a wage which lies approximately \$64275.27 away from the mean of \$54482.52.
This large standard deviation tells us that there is high variation between wage observations and that some of them are spread out very far from the mean, suggesting we have it is likely we have a lot of outliers in the data set (this is common for wage distribution in the presence of income inequality). This brings us to a general rule: the standard deviation is small when the data are all concentrated close to the mean, while the standard deviation is large when the data are spread out away from the mean.
Empirical Rule
Recall again from the Central Tendency notebook that data often approximately follow a normal distribution (symmetrical distribution wherein the mean value is also the median). For a variable with values distributed in this way, there is a standard when discussing their standard deviation. We say that about 68% of these values are within 1 standard deviation of the mean, about 95% are within 2 standard deviations of the mean, and about 99.7% are within 3 standard deviations from the mean. Remaining observations are extreme outliers and incredibly rare. This is called the 68-95-99.7 rule or Empirical Rule, and is visualized in the diagram below.

This gives us a helpful frame of reference when discussing the standard deviation of a variable. Although we already saw that the wages variable follows a relatively skewed distribution, we can imagine a variable that doesn’t - for example: test scores. If the mean score on a test is 70 and the standard deviation is 10, this tells us that approximately 68% of students who wrote that test earned a score between 60 and 80 (1 standard deviation), approximately 95% earned a score between 50 and 90 (2 standard deviations) and virtually everyone earned a score between 40 and 100 (3 standard deviations).
Understanding Measures of Dependence
Measures of dependence compute relationships between variables. The two most common measures of the relation between variables are covariance and correlation. We will investigate each of these, one at a time.
Covariance
Covariance is a measure of the direction of a relationship between two variables. More specifically, it can be broken down into a positive case (meaning the two variables are positively related) and a negative case (meaning the two variables are negatively related). If two variables are positively related, it means that when one goes up, we can expect the other to go up, and vice versa when one goes down. If two variables are negatively related, it means that when one goes up, the other goes down and vice versa. It is similar to the idea of variance that we just covered, but where variance measures how a single variable varies, covariance measures how two variables vary together.
Sample Covariance:
\[ cov_{x,y}=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{n-1} \]
Population Covariance:
\[ cov_{x,y}=\int\int(x_{i}-\bar{x})(y_{i}-\bar{y})f(x,y)dxdy \]
Note: As mentioned above, in R, the data only represents a sample. This is why we use n - 1 as a denominator, where n is the number of observations. When dealing with samples, the denominator has the freedom to vary (Degrees of Freedom). We only know sample means for both variables, so we use n - 1 to make the estimator unbiased, because n and n - 1 would be roughly equal for very large samples.
This is incredibly tedious to calculate, especially for large samples. In R, we can use the cov() function to calculate the covariance between two variables. Let’s say we’re interested in exploring the covariance between the wages variable and mrkinc variable in the dataset.
# cov() function requires use="complete.obs" to remove NA entries
cov(census_data$wages, census_data$mrkinc, use="complete.obs") The calculated covariance between the wages variable and mrkinc variable in the dataset is positive, indicating the two variables are positively related. As one variable changes, the other variable will change in the same direction with a magnitude of 4798121947.03. However, the wide range of calculated covariance makes it hard to interpret. In our example, covariance could return a value of 100, or 4798121947.03. This wide range of values is cause by a simple fact: The larger the X and Y values, the larger the covariance. A value of 100 or 4798121947.03 tells us that two variables are related, but that number does not tell us exactly how strong that relationship is.
Now, let’s try computing the covariance “by hand” to understand how the formula really works. To simplify the process, we will construct a hypothetical data set with variables x and y.
x <- c(6, 8, 10)
y <- c(25, 100, 125)# Difference of each value and the mean for the variables
# Product of the above differences
# Sum the products
# Denominator is one less than the sample size
sum((x - mean(x))*(y - mean(y)))/(3-1)# Confirming the previous calculation
cov(x,y)Covariance as a measure of dependence is not very meaningful. However, it is a computational stepping stone to something that is more interesting and informative, like correlation as we will see next. The correlation coefficient will tell us exactly how strong that relationship is by dividing the covariance by the standard deviation.
Correlation
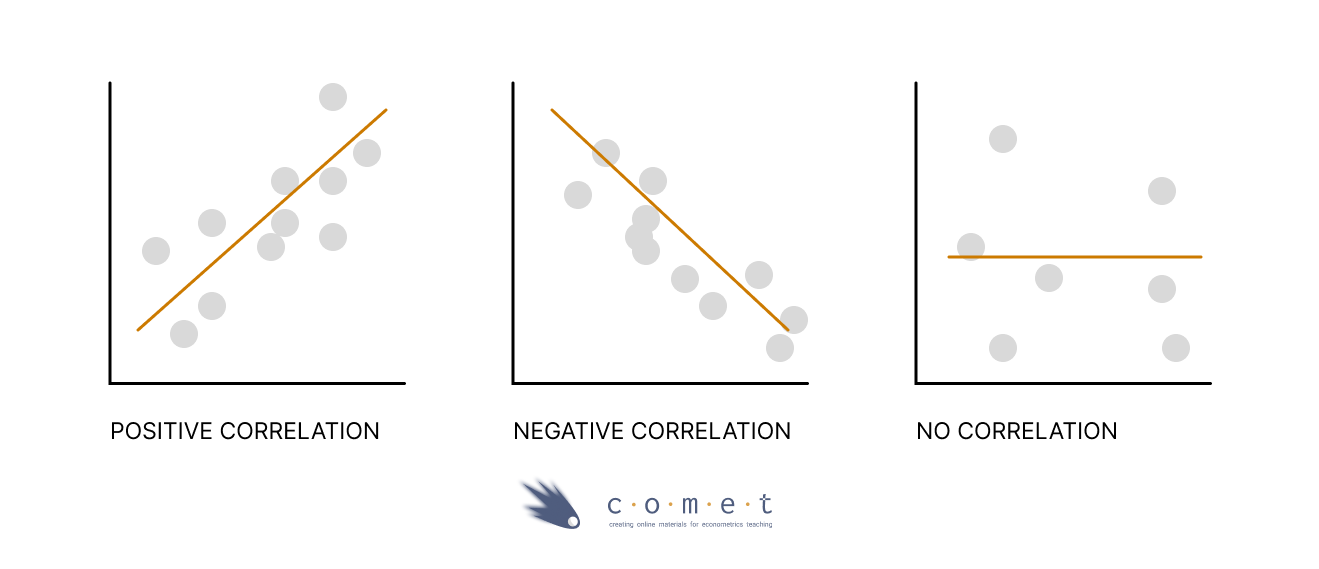
A correlation coefficient measures the linear relationship between two variables. It allows us to know if two variables evolve in the same direction (positive correlation), or in the opposite direction (negative correlation), or they are independent (no correlation).
Note that even though a covariance value or correlatation coefficient may have a value of 0, this does not mean that there is no relationship at all - this only means that there is no linear relationship between the two variables at hand.
Correlation standardizes covariance on a scale of -1 to 1 by dividing the covariance by the standard deviation. In this course, we use Pearson’s correlation coefficient which is calculated via the following formula:
\[ r_{x,y} = \frac{\sum_{i=0}^{n} (x_i - \overline{x})(y_i - \overline{y})}{\sqrt{\sum_{i=0}^{n} (x_i - \overline{x})^2 \sum_{i=0}^{n}(y_i - \overline{y})^2}}=\frac{cov_{x,y}}{s_{x} s_{y}} \]
Once again, let’s try to compute the correlation “by hand” using the formula.
numerator <- sum((x - mean(x))*(y - mean(y)))
denominator <- sqrt(sum((x - mean(x))^2) * sum((y - mean(y))^2))
numerator/denominatornumerator <- cov(x,y)
denominator <- sd(x) * sd(y)
numerator/denominatorIn R, we can use the cor() function to calculate the correlation between two variables
# Confirming the previous calculation
cor(x,y)To calculate the correlation between the wages variable and mrkinc variable in the dataset:
# cor() function requires use="complete.obs" to remove NA entries
cor(census_data$wages, census_data$mrkinc, use="complete.obs") Now we have the number 0.8898687 \(\approx\) 0.89 as our correlation coefficient. What does it really mean? Let’s start interpreting this number! First of all, a correlation coefficient ranges from -1 to 1, which tells us two things:
- The direction of the relationship between the 2 variables
- A negative correlation coefficient implies that the two variables evolve in opposite directions, that is, if a variable increases the other decreases and vice versa. A positive correlation, on the other hand, implies that the two variables evolve in the same direction, that is, if one variable increases the other also increases and vice versa.
- The strength of the relationship between the 2 variables
- The more extreme the correlation coefficient (the closer to -1 or 1), the stronger the relationship. The less extreme the correlation coefficient (the closer to 0), the weaker the relationship. Two variables are independent if the correlation coefficient is close to 0, that is, as one variable increases, there is no tendency in the other variable to either decrease or increase.
Test your knowledge
True or False? The correlation can measure linear relationship but the covariance can’t.
answer_5 <- "..." # enter True or False
test_5()We can also easily visualize correlation by plotting scatter plot with a trend line via ggplot() function.
ggplot(census_data, aes(x = mrkinc, y = wages)) +
geom_point(shape = 1)Adding a trend line to the scatter plot helps us interpret the directionality of two variables. We can do it via the geom_smooth() function by including the method=lm argument, which displays scatterplot patterns in the presence of overplotting. You will learn more about how trend lines are mathematically formulated in advanced econometrics classes.
ggplot(census_data, aes(x = mrkinc, y = wages)) +
geom_point(shape = 1) +
geom_smooth(method = lm)Now we can see the apparent positive correlation!
Try it yourself!
Brainstorm some real-world examples that best demonstrate the correlation relationships below. The first one is already done for you!
- zero or near zero : the number of forks in your house vs the average rainfall where you live
- weak negative: [your text here]
- strong positive: [your text here]
- weak positive: [your text here]
- strong negative: [your text here]
Making Tables: Visualizing Results
Tables can be a useful way to generate large lists of different statistics that are relevant to your analysis.
census_data <- census_data %>% drop_na(wages)table2 <- census_data %>%
group_by(immstat) %>% # we're intereseted in calculating different statistics based on immigration status (1 or 2: 1 = immigrant, 2 = non-immigrant)
summarize(avg_wage = mean(wages), # this will calulate all statistics two times, once for each group
sd_wage = sd(wages),
median_wage = quantile(wages,0.5),
r_wm = cor(wages, mrkinc))
table2A Note on Reshaping Tables
These tables can be tough to read. Fortunately, R has a nice set of reshaping commands which allow you to reorganize these tables:
pivot_wider: turn selected row-values into columns (usually what you want to do)
pivot_longer: turn selected columns into rows
You do this by specifying what the new names and rows should looks like. Here’s an example, using the above table:
pivot_wider(table2,
names_from = c(immstat),
values_from = c(avg_wage, sd_wage, median_wage, r_wm),
names_sep = ".") #the divider for new variable namesPractice Exercises
Exercise 1
Suppose the weights of packages(in lbs) at a particular post office are recorded as below. Assuming the weights follow a normal distribution.
package_data <- c(95, 130, 148, 183, 100, 98, 137, 110, 188, 166)# calculate the mean, standard deviation and variance of the weights of packages
# round all answers to 2 decimal places
answer_1 <- # enter your answer here for mean
answer_2 <- # enter your answer here for standard deviation
answer_3 <- # enter your answer here for variance
test_1()
test_2()
test_3()Exercise 2
Use the example above to answer: 68% of packages at the post office weigh how much? 1. A - 68% of packages weigh between 65.30 and 150.70 lbs 2. B - 68% of packages weigh between 100.40 and 170.60 lbs 3. C - 68% of packages weigh between 120.40 and 150.60 lbs 4. D - 68% of packages weigh between 80.56 and 120.60 lbs
answer_4 <- "..." # enter your choice here (ex, "F")
test_4()